Шапка

(27065) Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.

Задача 1

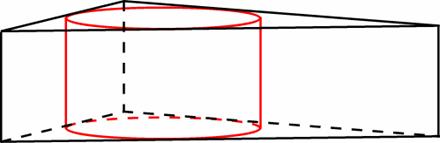
Дано:
Ф1 – призма, описанная
Ф2 – цилиндр, вписанный
ABC – треугольник : AB = BC = AC
AA1 ⊥ (ABC)
rц = √3 Hц = 2

Найти:
S б п п



Решение:

1. Sб п п = Pо⋅H = 3⋅a3⋅H
Т.к. цилиндр вписан в призму, то:
1. Hц = Hпр = 2
2. Основание цилиндра – круг – вписан в основание призмы – правильный треугольник, т.е.
а3 = 2√3rц = 2√3⋅√3 = 2⋅3=6.
Итак, Sб п п = 3⋅6⋅2=36.
Ответ: 36.

(73015) Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √75, а высота равна 4.

Задача 2

Дано:
Ф1 – призма, описанная
Ф2 – цилиндр, вписанный
ABC – треугольник : AB = BC = AC
AA1 ⊥ (ABC)
rц = √75 Hц = 4

Найти:
S б п п



Решение:

1. Sб п п = Pо⋅H =
Т.к. цилиндр вписан в призму, то:
1. Hц = Hпр =
2. Основание цилиндра – – вписан в основание призмы – , т.е.
а3 = ⋅rц = .
Итак, Sб п п =3⋅ ⋅ =.
Ответ: .

Заполнять решение необходимо так же, как и в образце, с полным соблюдением порядка и знаков, необходимо писать без пробелов (4⋅a⋅H) и используя знак умножения (⋅).

(73021) Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √0.12, а высота равна 1.

Ответ: .